Планы-конспекты лекционных занятий

, , , . (*)

Где 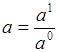, ,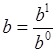,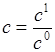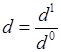. Поскольку, сложное отношение точек не зависит от выбора репера, то в качестве репера можно выбрать репер , тогда будут являться аффинными координатами на данной прямой.

Найдем простое отношение (используя определение простого отношения): , .

Найдем сложное отношение по формуле (1), используя координаты (*):

.

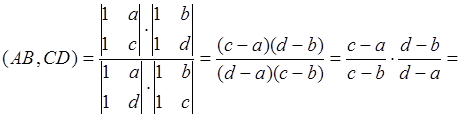
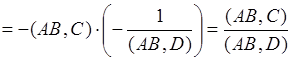Замечание 1. Несобственная точка делит любой отрезок прямой в отношении , то есть .

Замечание 2. Если выбрать в качестве репера , то в этом репере точка будет иметь координаты: . Зная сложное отношение точек , всегда можно найти расположение точки на прямой. В этом случае .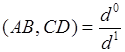

Значит, если , то .

2. Свойства сложного отношения четырех точек

10:

Сложное отношение точек не изменится, если поменять местами пару точек: .

Доказательство: 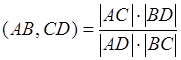, 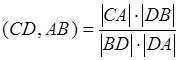. Учитывая, что получим, что . Свойство доказано.

20:

Сложное отношение точек меняет свое значение на обратное, при перестановке точек внутри одной пары: .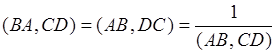

Доказательство: 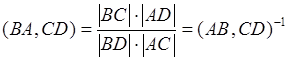, 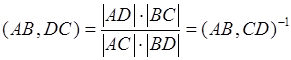. Свойство доказано.

30:

Если поменять местами точки внутри каждой пары, то сложное отношение не изменится: .

Доказательство: следует из свойства 20. 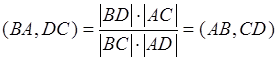. Свойство доказано.

40:

.

Доказательства первого, второго и третьего свойства предложить студентам на самостоятельное изучение.

Замечание. Пусть на прямой заданы точки , тогда