Планы-конспекты лекционных занятий

На проективной плоскости возьмем репер и произвольную точку . Пусть – проекции точек и на прямую из центра . Мы знаем, что в репере на прямой точка имеет координаты и, следовательно, по формуле (2) 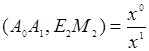при условии, что , то есть . Аналогичные выражения получим и для других отношений между координатами точки . Поэтому справедлива

Теорема 4.

Если точка имеет координаты относительно репера проективной плоскости, то отношение 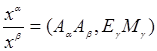равно сложному отношению четырех точек: двух вершин , и проекций , на прямую точек и из третьей вершины координатного треугольника (при условии, что , т. е. ) [3].

4.Итог занятия.

Итак, сегодня мы познакомились с понятием сложного отношения четырех точек прямой, изучили свойства сложного отношения, рассмотрели сложное отношение четырех прямых пучка.

– Как обозначается сложное отношение четырех точек прямой?

Возможный вариант ответа: (AB,CD).

– Какие свойства сложного отношения точек сегодня были изучены?

– Каким отношением связанно сложное отношение четырех точек прямой и отношение трех точек прямой?

– При обозначении сложного отношения точек важен порядок записи точек?

Лекция № 2

Тема: Полный четырехвершинник

Цель: обучающая: ввести определение гармонической четверки точек, изучить теорему о свойствах полного четырехвершинника;

развивающая: развивать память, логическое мышление, умение анализировать, выделять закономерности, обобщать, способность быстро ориентироваться в ситуации;

воспитательная: воспитывать положительное отношение к процессу обучения, уважение к сверстникам и преподавателю.

Тип занятия: лекция.

Структура занятия:

1.Организационный момент (2 мин).

2.Изложение нового материала (85 мин).

3.Итог занятия (3 мин).

Ход занятия

1.Организационный момент.

- преподаватель здоровается и отмечает отсутствующих студентов;

- сообщается тема занятия, его цель: На этой лекции мы познакомимся с понятием гармонической четверки точек, изучим теорему о свойствах полного четырехвершинника.